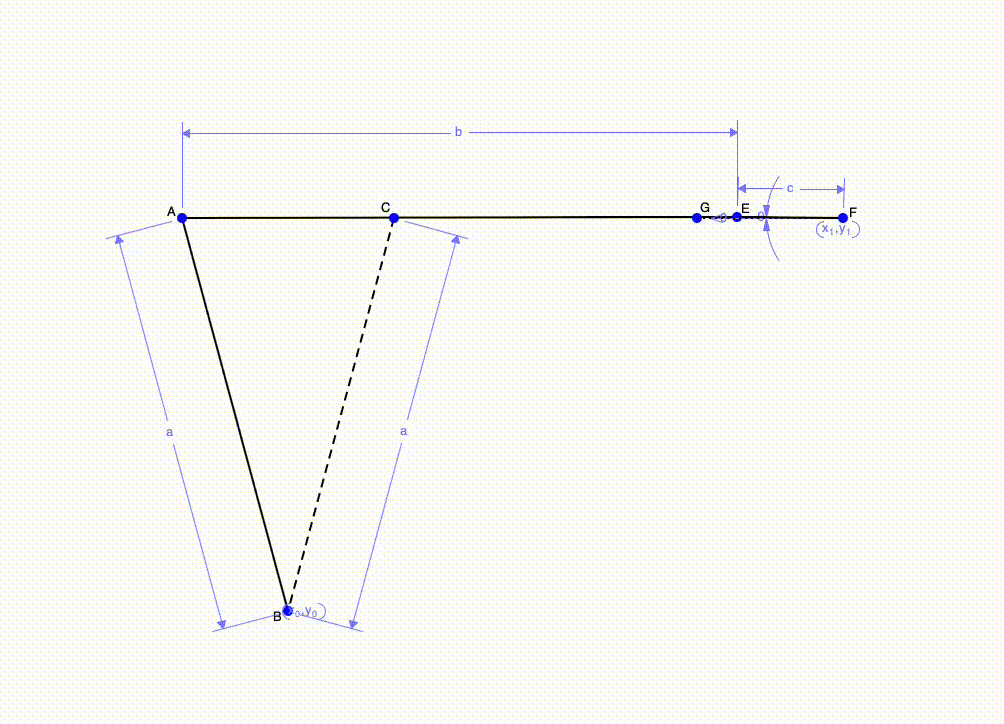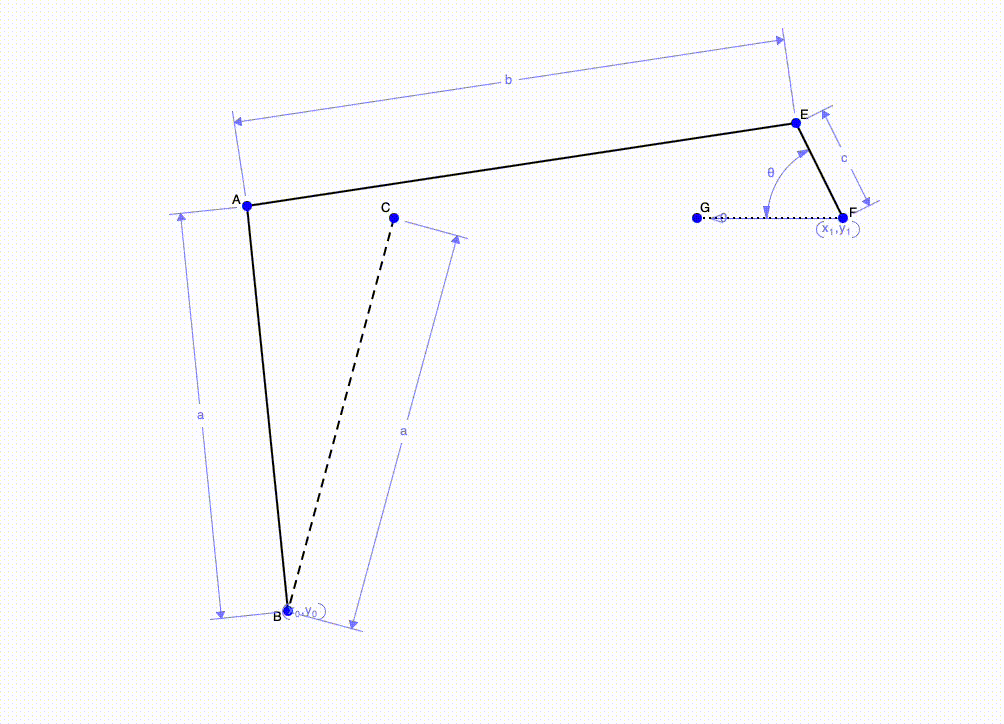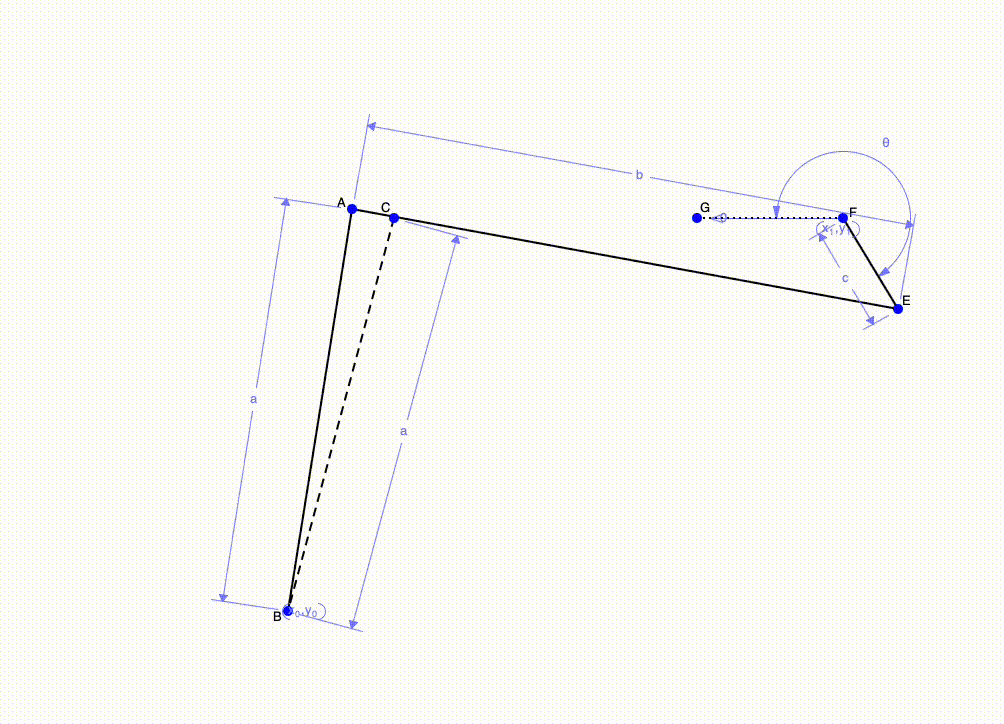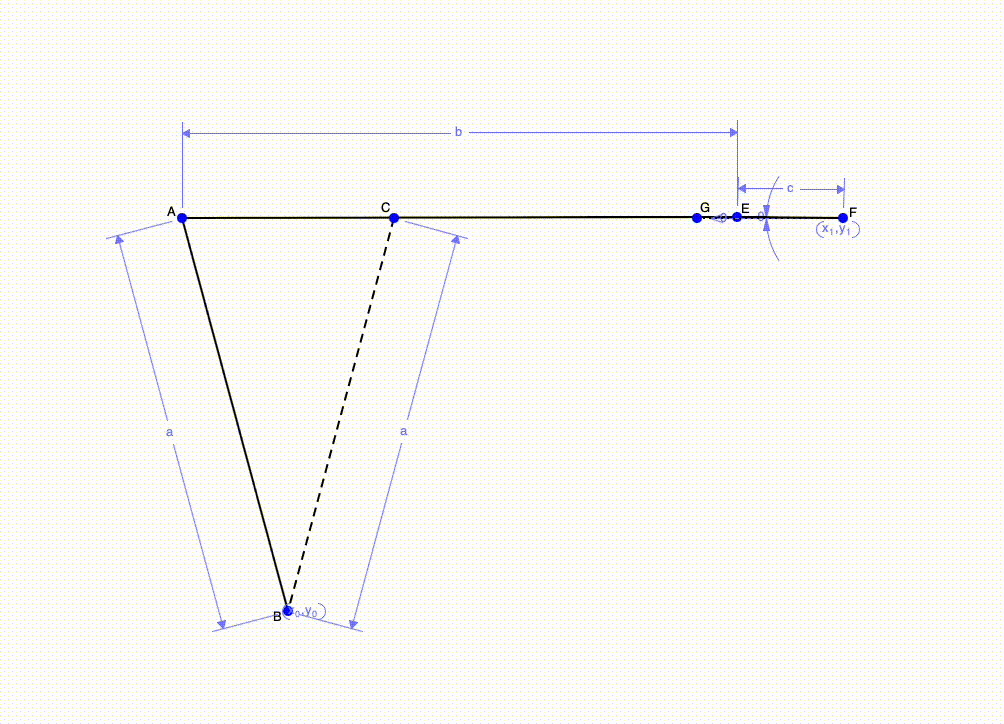
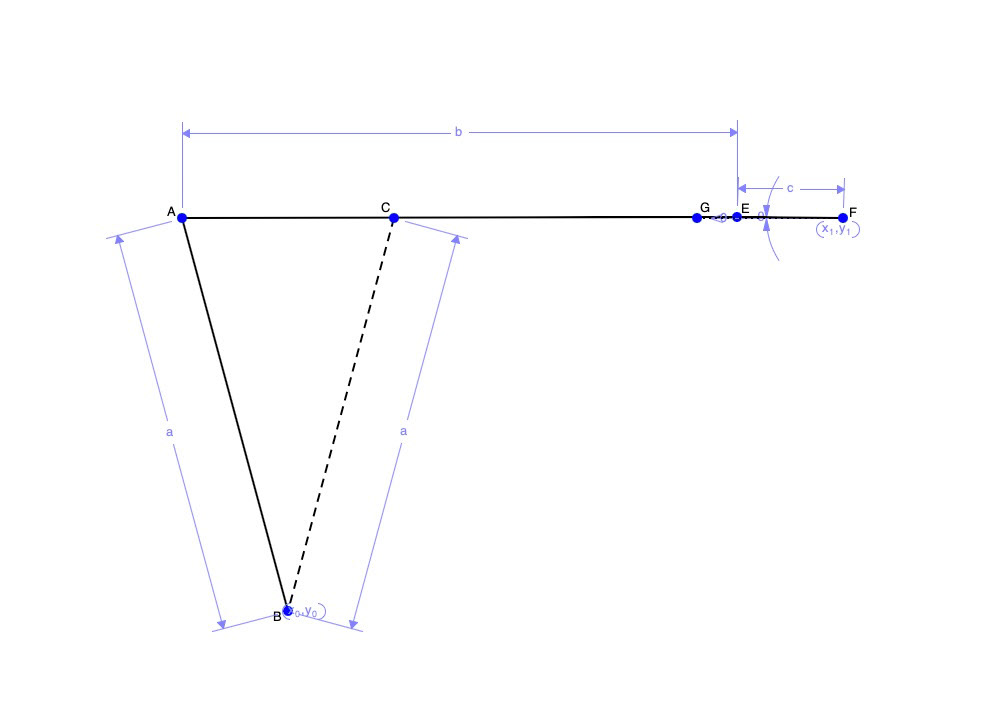
Above is an example of a rocker mechanism with pure rotation. This is when we want to rotate a beam about a fixed point. To construct this mechanism, the length of the crank must be half the distance of the two end points of the beam. In the picture above, the crank is line EF. Thus, EF is half the length of AC. Placing the crank in line with AC will allow us to have the same speed during both forward and return. If we position F above or below AC, this will change the speed of the forward and return motion. Lastly, the coupler (line AG) length is not important and only serves to connect the crank and the output (line AB)
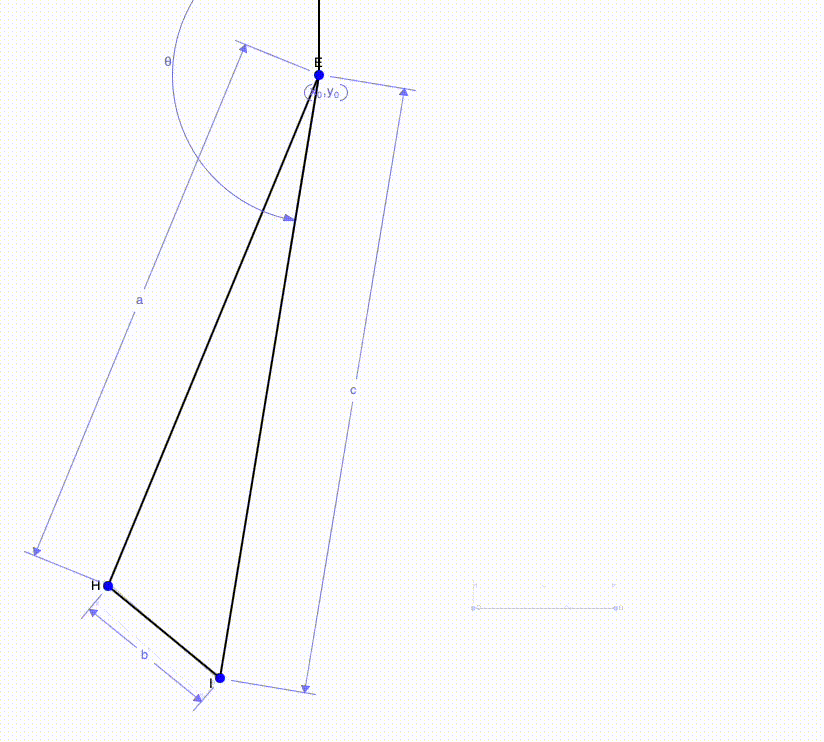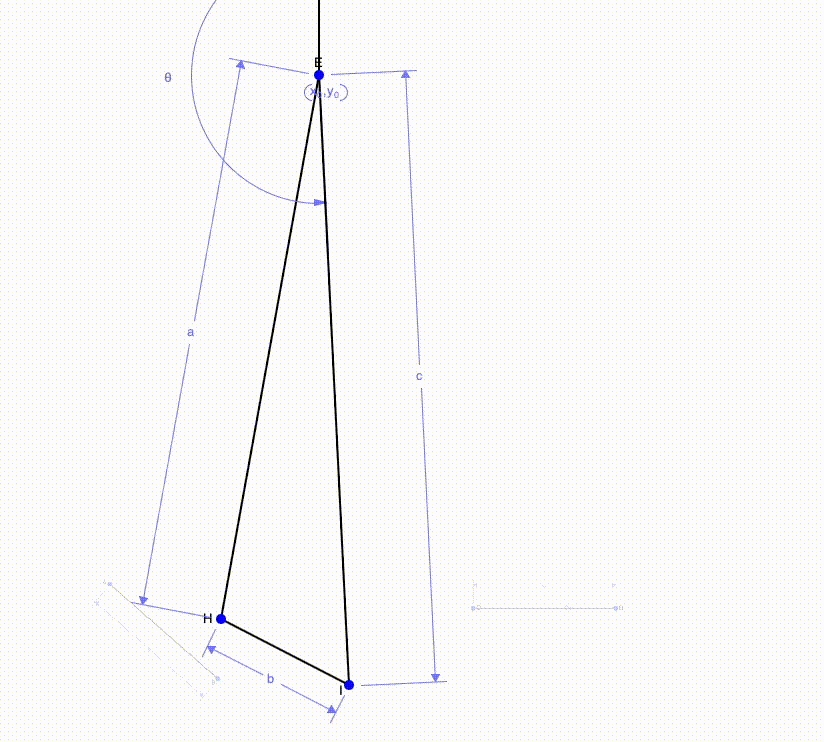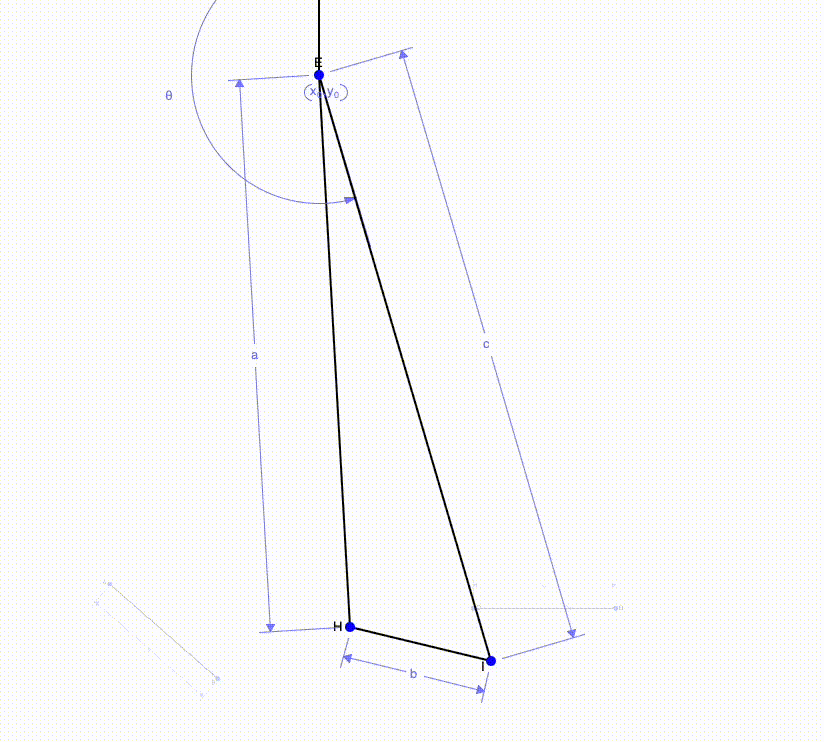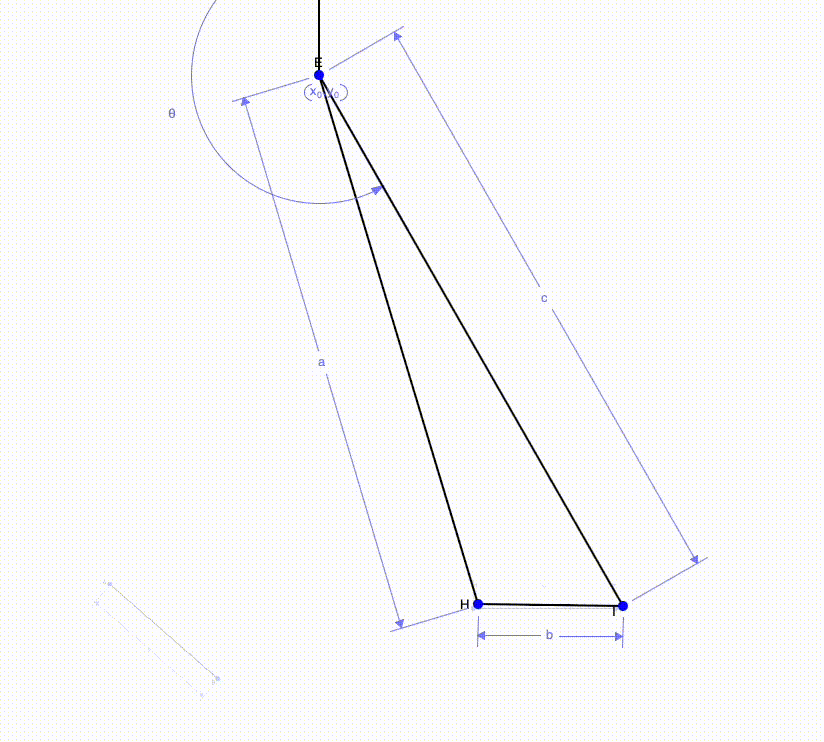
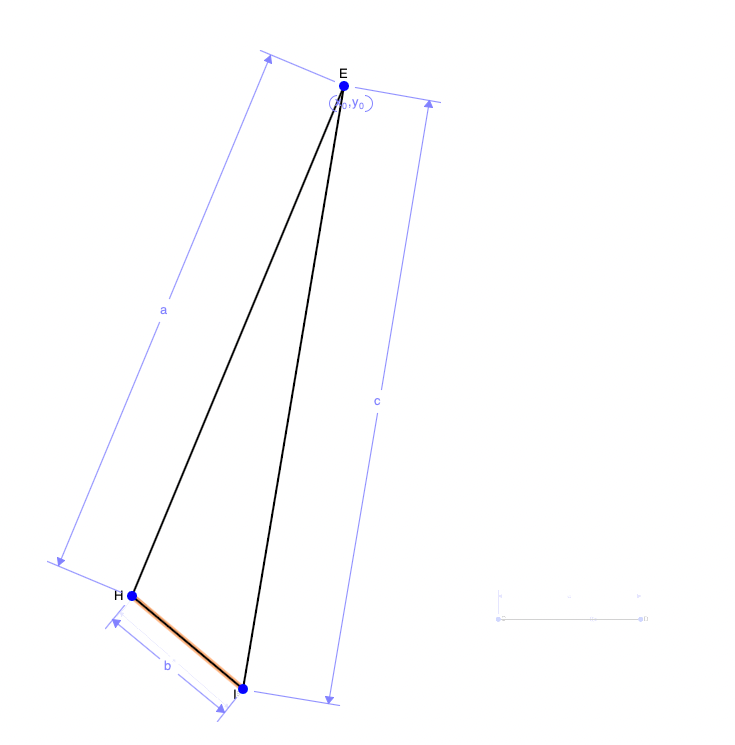
The images above show a multi-step motion (rotation + translation) can be simplified to one single motion. This can be done by finding the perpendicular bisectors of the initial and final position of each side of the beam. Using the intersection of the two perpendicular bisectors, we can add a third point (point E in the image) which is where the beam will rotation about. Finally, we can connect this point to the ends of the beam.
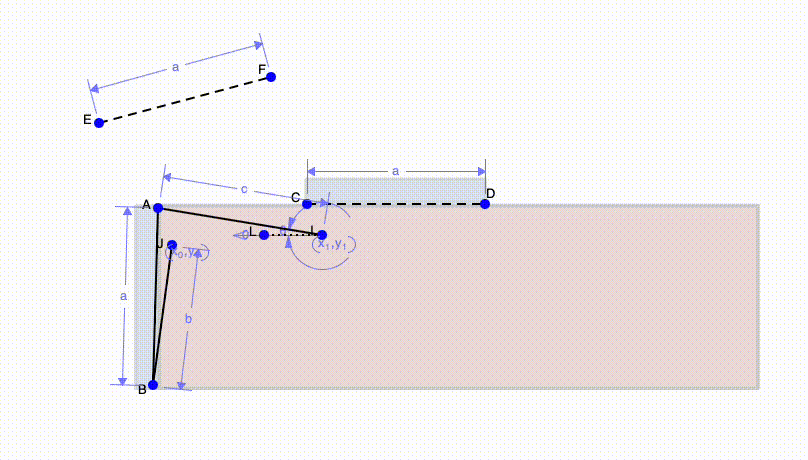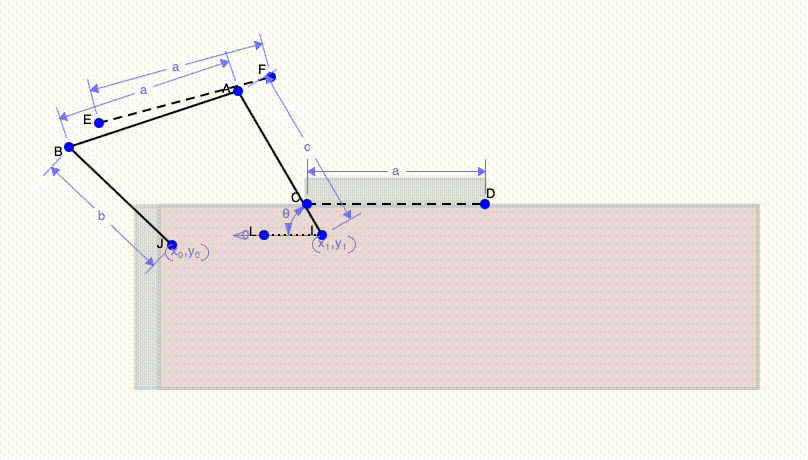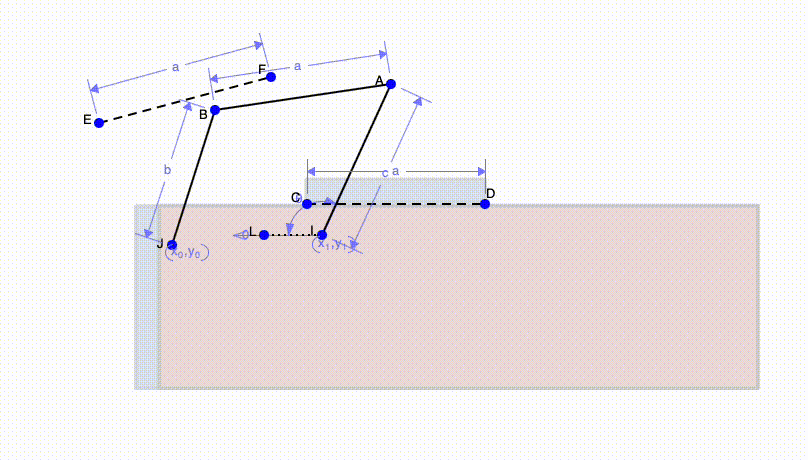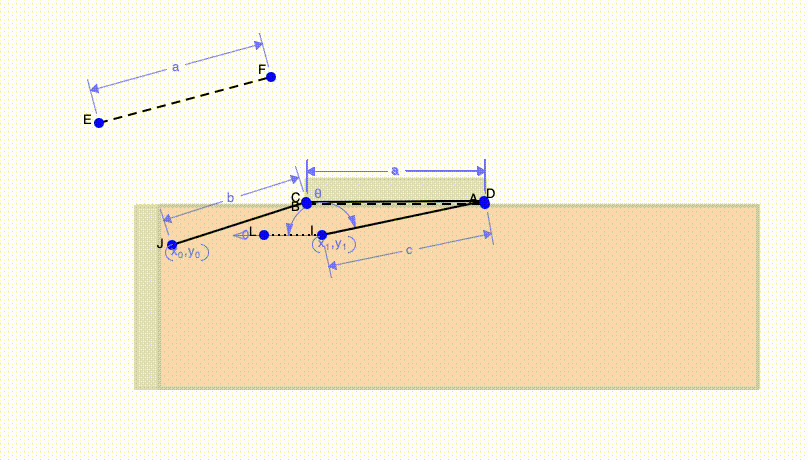
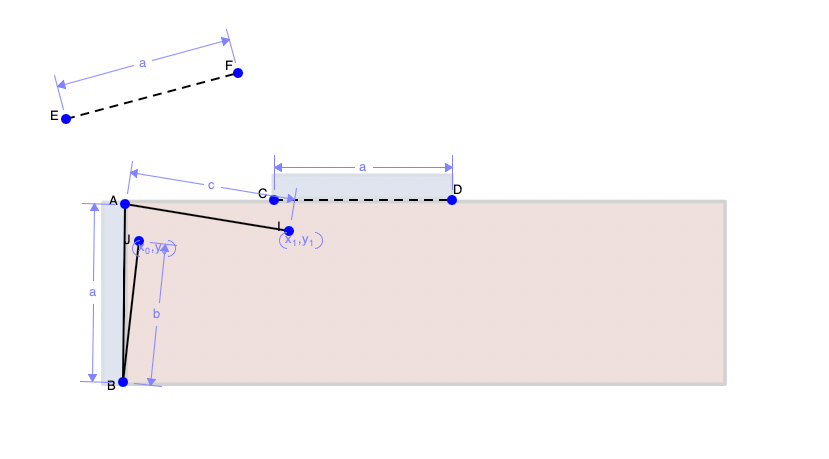
We can finally use these simple concepts to solve real world challenges. Above we have a shipping container. In order for the door of the shipping container to be able to rest on top, we must make sure it doesn't hit the corners of the container. To do this, I mark a third position in the middle of the initial and final position (line EF). This is so that I can ensure the door will avoid the corner of the container. Next I draw perpendicular bisectors and mark where they intersect for points BE and EC, then for points AF and FD. Lastly, I can connect the two points to the ends of the beam.